What property of objects is best measured by their capacitance?
the ability to conduct electric current
the ability to distort an external electrostatic field
the ability to store charge
Consider an air-filled charged capacitor. How can its capacitance be increased?
Increase the charge on the capacitor.
Decrease the charge on the capacitor.
Increase the spacing between the plates of the capacitor.
Decrease the spacing between the plates of the capacitor.
Increase the length of the wires leading to the capacitor plates.
Double the plate separation.
Check all that apply.Double the charge.
Double the plate area.
Double the plate separation.
Halve the charge.
Halve the plate area.
Halve the plate separation.
Consider a charged parallel-plate capacitor. Which combination of changes would quadruple its capacitance?
Double the charge and double the plate area.
Double the charge and double the plate separation.
Halve the charge and double the plate separation.
Halve the charge and double the plate area.
Halve the plate separation and double the plate area.
Double the plate separation and halve the plate area.
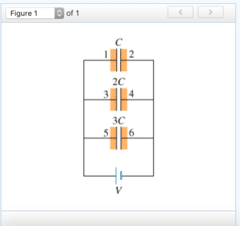
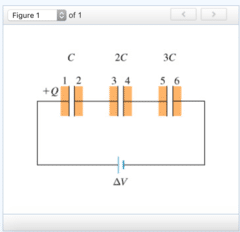
If the potential of plate 1 is V, then, in equilibrium, what are the potentials of plates 3 and 6? Assume that the negative terminal of the battery is at zero potential.
V and V
2V and 3V
V and 0
V2 and V3
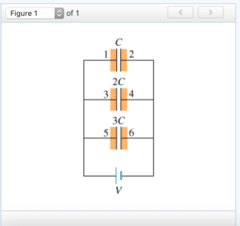
If the charge of the first capacitor (the one with capacitance C) is Q, then what are the charges of the second and third capacitors?
2Q and 3Q
Q2 and Q3
Q and Q
0 and 0
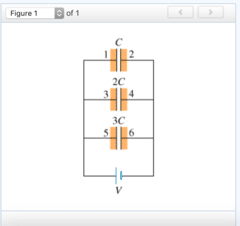
Express your answer in terms of V and C.
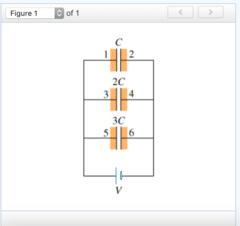
Express your answer in terms of C.
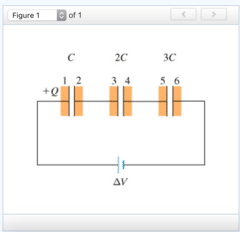
What are the charges on plates 3 and 6?
+Q and +Q
−Q and −Q
+Q and −Q
−Q and +Q
0 and +Q
0 and −Q
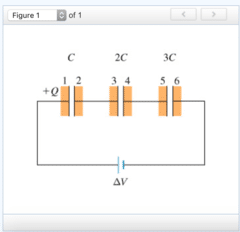
If the voltage across the first capacitor (the one with capacitance C) is ΔV1, then what are the voltages across the second and third capacitors?
2ΔV1 and 3ΔV1
1/2ΔV1 and 1/3ΔV1
ΔV1 and ΔV1
0 and ΔV1
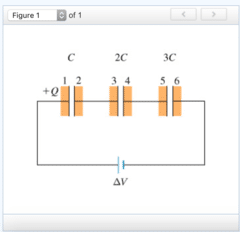
Express your answer in terms of ΔV.
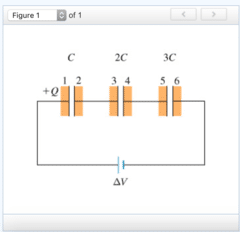
Express your answer in terms of C and ΔV1.
Express your answer in terms of C.
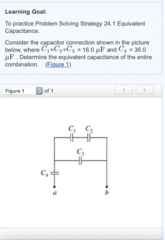
C1 is in series with C2.
Check all that apply.C4 is in series with C1 and C2.
C3 is in series with C4.
C3 is in parallel with C1 and C2.
C1 is in series with C2.
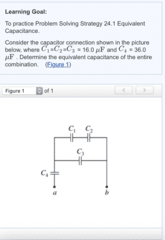
Express your answer in microfarads to three significant figures.
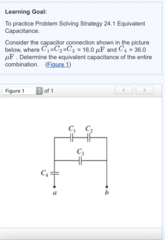
Suppose that you are given another network of the same form as the one analyzed in Part B, but with different values for the individual capacitances. How would you expect the equivalent capacitance Ceq to compare to the values of each individual capacitor in the network? Choose the statement below that is true regardless of the actual values for the individual capacitors.
Ceq must be less than C3.
The value of Ceq is not bounded by the value of any individual capacitance in the network.
Ceq must be less than C4.
Ceq must be less than C1+C2 .
If the spacing between the plates, d, is the same in both capacitors, and the voltage across capacitor 1 is V, what is the voltage across capacitor 2?V/2
V
2V
4V
If the spacing between the plates in capacitor 1 is d, what should the spacing between the plates in capacitor 2 be to make the capacitance of the two capacitors equal?d/2
d
2d
4d
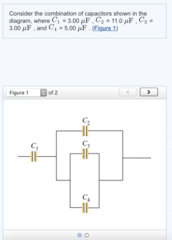
Express your answer in microfarads.
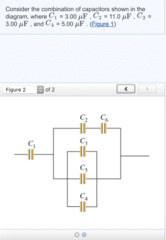
Express your answer in microfarads.
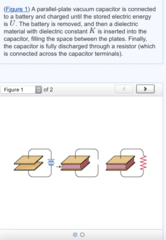
Express your answer in terms of U and other given quantities.
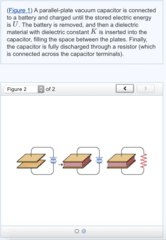
Express your answer in terms of U and other given quantities.
A spherical capacitor is formed from two concentric spherical conducting shells separated by vacuum. The inner sphere has radius 10.0 centimeters, and the separation between the spheres is 1.50 centimeters. The magnitude of the charge on each sphere is 3.30 nanocoulomb.
What is the magnitude of the potential difference ΔV between the two spheres?
A spherical capacitor is formed from two concentric spherical conducting shells separated by vacuum. The inner sphere has radius 10.0 centimeters, and the separation between the spheres is 1.50 centimeters. The magnitude of the charge on each sphere is 3.30 nanocoulomb.
What is the electric-field energy stored in the capacitor?
Find the energy U0 stored in the capacitor.Express your answer in terms of A, d, V, and ϵ0.
An air-filled parallel-plate capacitor has plate area A and plate separation d. The capacitor is connected to a battery that creates a constant voltage V.
The capacitor is now disconnected from the battery, and the plates of the capacitor are then slowly pulled apart until the separation reaches 3d. Find the new energy U1 of the capacitor after this process.
Express your answer in terms of A, d, V, and ϵ0.
An air-filled parallel-plate capacitor has plate area A and plate separation d. The capacitor is connected to a battery that creates a constant voltage V.
The capacitor is now reconnected to the battery, and the plate separation is restored to d. A dielectric plate is slowly moved into the capacitor until the entire space between the plates is filled. Find the energy U2 of the dielectric-filled capacitor. The capacitor remains connected to the battery. The dielectric constant is K.
Express your answer in terms of A, d, V, K, and ϵ0.
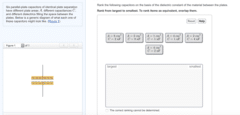
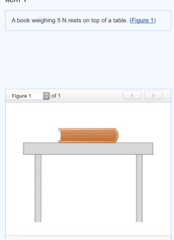
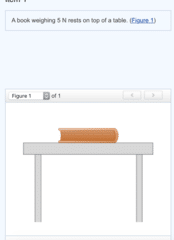
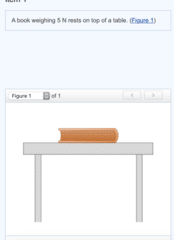
A downward force of magnitude 5 N is exerted on the book by the force of
the table
gravity
inertia
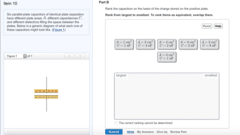
Newton’s 2nd law
Check all that apply.Newton’s 1st law
Newton’s 2nd law
Newton’s 3rd law
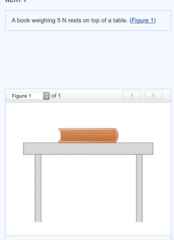
Check all that apply.Newton’s 1st law
Newton’s 2nd law
Newton’s 3rd law
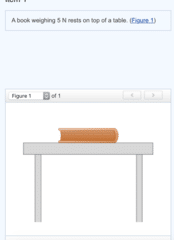
First, consider a book resting on a horizontal table.
Which object exerts a downward force on the book?
the book itself
the earth
the surface of the table
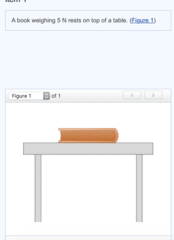
First, consider a book resting on a horizontal table.
The downward force acting on the book is __________.
a contact force
a long-range force
What is the downward force acting on the book called?tension
normal force
weight
friction
First, consider a book resting on a horizontal table.
Which object exerts an upward force on the book?
the book itself
the earth
the surface of the table
The upward force acting on the book is __________.a contact force
a long-range force
What is the upward force acting on the book called?tension
normal force
weight
friction
Which object exerts a force on the block that is directed toward the right?the block itself
the earth
the surface of the table
the string
The force acting on the block and directed to the right is __________.a contact force
a long-range force
What is the force acting on the block and directed to the right called?tension
normal force
weight
friction
Which object exerts a force on the block that is directed toward the left?the block itself
the earth
the surface of the table
the string
The force acting on the block and directed to the left is __________.a contact force
a long-range force
What is the force acting on the block and directed to the left called?tension
normal force
weight
friction
How many forces are acting on the block in the horizontal direction?0
1
2
3
The same block is placed on the same rough table. However, this time, the string is disconnected and the block is given a quick push to the right. The block slides to the right and eventually stops. The following questions refer to the motion of the block after it is pushed but before it stops.
What is the force acting on the block that is directed to the left called?
tension
normal force
weight
friction
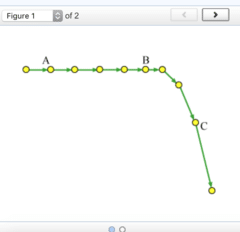
What is the direction of the net force acting on the object at position A?
upward
downward
to the left
to the right
The net force is zero.
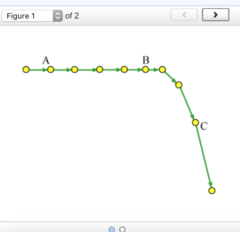
What is the direction of the net force acting on the object at position B?
upward
downward
to the left
to the right
The net force is zero.
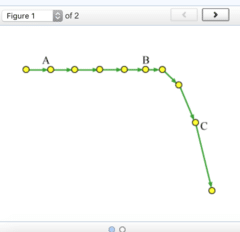
What is the direction of the net force acting on the object at position C?
upward
downward
to the left
to the right
The net force is zero.
A hockey puck slides along a horizontal icy (frictionless) surface.
A car is moving along a straight road at a constant speed.
A car is moving along a straight road while slowing down.
A car is moving along a straight road while speeding up.
A hockey puck slides along a horizontal icy (frictionless) surface.
A hockey puck slides along a rough concrete surface.
A cockroach is speeding up from rest.
A rock is thrown horizontally; air resistance is negligible.
A rock is thrown horizontally; air resistance is substantial.
A rock is dropped vertically; air resistance is negligible.
A rock is dropped vertically; air resistance is substantial.Which of these situations describe the motion shown in the motion diagram at point A?
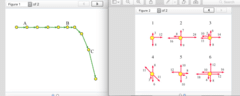
A hockey puck slides along a rough concrete surface.
A car is moving along a straight road at a constant speed.
A car is moving along a straight road while slowing down.
A car is moving along a straight road while speeding up.
A hockey puck slides along a horizontal icy (frictionless) surface.
A hockey puck slides along a rough concrete surface.
A cockroach is speeding up from rest.
A rock is thrown horizontally; air resistance is negligible.
A rock is thrown horizontally; air resistance is substantial.
A rock is dropped vertically; air resistance is negligible.
A rock is dropped vertically; air resistance is substantial.Which of these situations describe the motion shown in the motion diagram at point B?
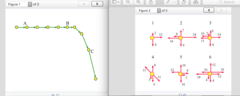
A car is moving along a straight road at a constant speed.
A car is moving along a straight road while slowing down.
A car is moving along a straight road while speeding up.
A hockey puck slides along a horizontal icy (frictionless) surface.
A hockey puck slides along a rough concrete surface.
A cockroach is speeding up from rest.
A rock is thrown horizontally; air resistance is negligible.
A rock is thrown horizontally; air resistance is substantial.
A rock is dropped vertically; air resistance is negligible.
A rock is dropped vertically; air resistance is substantial.
Which of these situations describe the motion shown in the motion diagram at point C?
F3 on 1, F1 on 3, F2 on 1, F1 on 2, F3 on 2, F2 on 3, F1 on floor, Floor on F1

F3 on 1, F1 on 3, F2 on 1, F1 on 2, F3 on 2, F2 on 3, F1 on floor, Floor on F1
An object cannot remain at rest unless which of the following holds?
The net force acting on it is zero.
The net force acting on it is constant and nonzero.
There are no forces at all acting on it.
There is only one force acting on it.
If a block is moving to the left at a constant velocity, what can one conclude?
There is exactly one force applied to the block.
The net force applied to the block is directed to the left.
The net force applied to the block is zero.
There must be no forces at all applied to the block.
A block of mass 2kg is acted upon by two forces: 3N (directed to the left) and 4N (directed to the right). What can you say about the block’s motion?
It must be moving to the left.
It must be moving to the right.
It must be at rest.
It could be moving to the left, moving to the right, or be instantaneously at rest.
A massive block is being pulled along a horizontal frictionless surface by a constant horizontal force. The block must be __________.
continuously changing direction
moving at constant velocity
moving with a constant nonzero acceleration
moving with continuously increasing acceleration
Check all that apply.cannot have a magnitude equal to 5N
cannot have a magnitude equal to 10N
cannot have the same direction as the force with magnitude 10N
must have a magnitude greater than 10N

Every force has one and only one 3rd law pair force.
true
false
The two forces in each pair act in opposite directions.
true
false
The two forces in each pair can either both act on the same body or they can act on different bodies.
true
false
The two forces in each pair may have different physical origins (for instance, one of the forces could be due to gravity, and its pair force could be due to friction or electric charge).
true
false
The two forces of a 3rd law pair always act on different bodies.
true
false
Given that two bodies interact via some force, the accelerations of these two bodies have the same magnitude but opposite directions. (Assume no other forces act on either body.)
true
false
According to Newton’s 3rd law, the force on the (smaller) moon due to the (larger) earth is
greater in magnitude and antiparallel to the force on the earth due to the moon.
greater in magnitude and parallel to the force on the earth due to the moon.
equal in magnitude but antiparallel to the force on the earth due to the moon.
equal in magnitude and parallel to the force on the earth due to the moon.
smaller in magnitude and antiparallel to the force on the earth due to the moon.
smaller in magnitude and parallel to the force on the earth due to the moon.
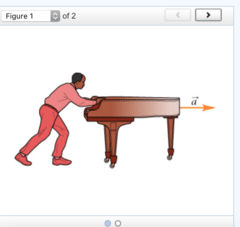
Chadwick is pushing a piano across a level floor (see the figure). (Figure 1) The piano can slide across the floor without friction. If Chadwick applies a horizontal force to the piano, what is the piano’s acceleration?
To solve this problem you should start by drawing a free-body diagram.Determine the object of interest for the situation described in the problem introduction.
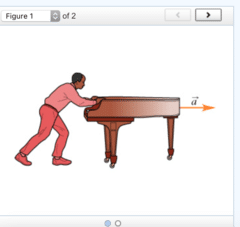
force of the floor on the piano (normal force)
force of Chadwick on the piano
Chadwick is pushing a piano across a level floor (see the figure). (Figure 1) The piano can slide across the floor without friction. If Chadwick applies a horizontal force to the piano, what is the piano’s acceleration?
To solve this problem you should start by drawing a free-body diagram
Identify the forces acting on the object of interest. From the list below, select the forces that act on the piano.
Check all that apply.acceleration of the piano
gravitational force acting on the piano (piano’s weight)
speed of the piano
gravitational force acting on Chadwick (Chadwick’s weight)
force of the floor on the piano (normal force)
force of the piano on the floor
force of Chadwick on the piano
force of the piano pushing on Chadwick

Chadwick now needs to push the piano up a ramp and into a moving van. (Figure 2) The piano slides up the ramp without friction. Is Chadwick strong enough to push the piano up the ramp alone or must he get help? To solve this problem you should start by drawing a free-body diagram.
Determine the object of interest for this situation.

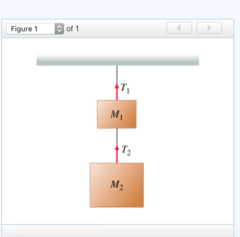
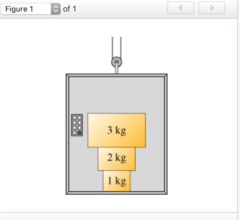
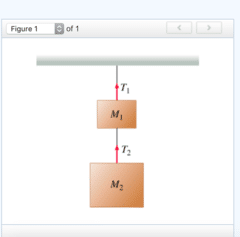
Find T2, the tension in the lower rope.
Find T1, the tension in the upper rope.
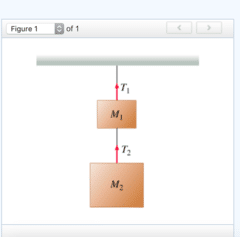
Find T2, the tension in the lower rope.
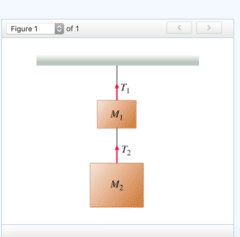
Find T1, the tension in the upper rope.



