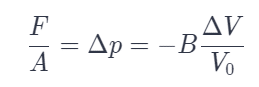A solid gold bar is pulled up from the hold of the sunken RMS Titanic.
(a) What happens to its volume as it goes from the pressure at the ship to the lower pressure at the ocean’s surface?
(b) The pressure difference is proportional to the depth. How many times greater would the volume change have been had the ship been twice as deep?
(c) The bulk modulus of lead is one-fourth that of gold. Find the ratio of the volume change of a solid lead bar to that of a gold bar of equal volume for the same pressure change.
Answer:
(a) The volume of the bar increases.
(b) The volume change would be twice as great.
(c) The volume change of the solid lead bar is four times as that of the gold bar.
Explanation
Concepts and Principles
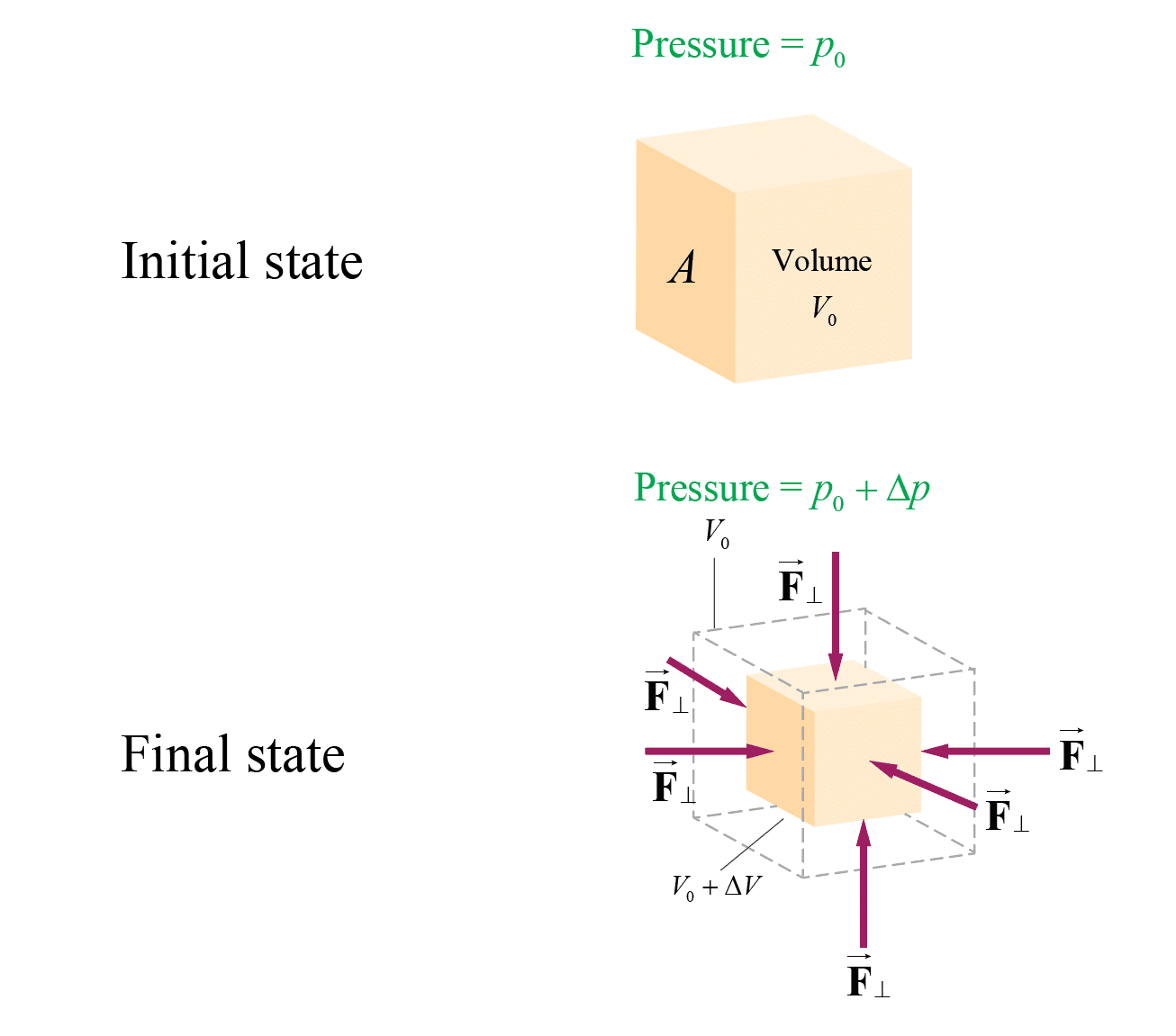
Bulk Modulus: it is used to describe the elastic behavior (deformations) of objects undergoing hydraulic compression due to a stress exerted by a surrounding fluid. When the pressure on a body changes by a small amount Delta P, from P0 to P0+Delta P, the strain (fractional change in volume) is linearly related to the applied stress (force per unit area) by the following relation
where Delta P is the additional pressure (hydraulic pressure) on the object due to the fluid, Delta V/V0 (the strain) is the fractional change in the object’s volume due to that pressure, and B is the Bulk modulus for the object. The negative sign ensures that the pressure is a positive number.
Compressibility, k, is the reciprocal of bulk modulus: k=1/B.
Given Data
- A solid gold bar is pulled up from water.
- The pressure at the ship is lower that the pressure at the ocean’s surface.
- The pressure difference is proportional to the depth.
- The bulk modulus of lead is one-fourth that of gold.
Required Data
In part (a), we are asked to determine what happens to the volume of the bar as it goes from the ship to the ocean’s surface.
In part (b), we are asked to determine how much the volume would change if the ship had been twice as deep.
In part (c), we are asked to determine the ratio of volume change of a solid lead bar to that of a gold bar of equal volume for the same pressure change.
Solution
(a)
According to Equation (*), the volume is inversely proportional to the change in volume. Since the pressure decreases (the change is negative), the volume of the bar increases (the change is positive) as it goes from the ship to the ocean’s surface.
(b)
The pressure difference is proportional to the depth, therefore, if the ship had been twice as deep, the pressure difference is twice as high. Hence, as the bar now goes from the ship to the ocean’s surface, the volume change would be twice as great.
(c)
The volume change is, according to Equation (*), inversely proportional to the bulk modulus of the material. And since the bulk modulus of lead is one-fourth that of gold, the volume change of the solid lead bar is four times as that of the gold bar.