Which Of The Following Is A Good Point Estimator For The Population Variance?
- S^2
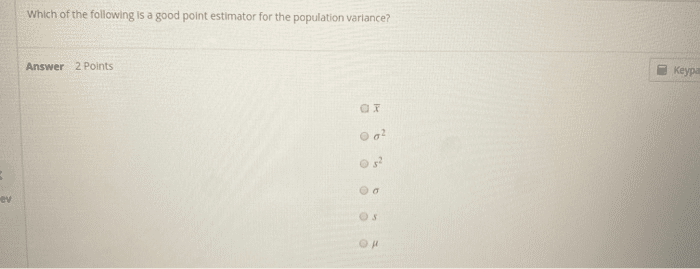
Which of the following is a good point estimator for the population variance?
S^2
For a quantitative variable in a particular population, how many different sample means are there?
Many
Which of the following is a good point estimator for the population standard deviation?
S
Which of the following is a good point estimator for the population mean?
x BAR
biased sample
A sample that does not fairly represent the population. A sample that overrepresents or underrepresents some segment(s) of the population
sampling frame
is a list which identifies all members of the population.
census
a count or measure of an entire population
sampling
a count or measure of part of a population and is more commonly used in statistical studies.
sampling error
the difference between the results of a sample and those of the population.
random sample
a sample that fairly represents a population because each member has an equal chance of inclusion
simple random sample
Every possible sample of the same size has the same chance of being selected
stratified sample
the population is divided into groups (strata) and a random sample is taken from each group (stratum)
cluster sample
Divide the population into groups (clusters) and select all of the members in one or more, but not all, of the clusters.
systematic sample
obtained by selecting every kth individual from the population. Choose a starting value at random. Then choose every kth member of the population.
convenience sample
Choose only members of the population that are easy to get.
Often leads to biased studies (not recommended).
Often leads to biased studies (not recommended).
sampling distribution of a statistic (such as the sample mean or sample proportion)
is the probability distribution of all values of the statistic when all possible samples of size n are taken from a population
point estimator
is a single-valued estimate calculated from the sample data, which is intended to be close to the true population value.
unbiased
If the average value of an estimator equals the population parameter being estimated, the estimator is said to be unbiased
standard error of the mean
is the standard deviation of a point estimator.
Central Limit Theorem
important theorem which summarizes the distribution of the sample mean. The distribution of the sample mean becomes closer to a normal distribution as the sample size becomes larger, regardless of the shape of the population for which the sample is drawn.
Which of the following is a good point estimator for the population variance?
Statistical inference uses statistics calculated from samples as the basis of an inference about the population. If the sample is representative, then the sample statistics (which are random variables that depend on which random sample is selected) ought to be close to their population counterparts. In other words, the sample mean ought to be close to the population mean, the sample proportion ought to be close to the population proportion, and the sample standard deviation should be close to the population standard deviation. Thus, a good point estimator for the population variance is s2.
Which of the following is a good point estimator for the population standard deviation?
Statistical inference uses statistics calculated from samples as the basis of an inference about the population. If the sample is representative, then the sample statistics (which are random variables that depend on which random sample is selected) ought to be close to their population counterparts. In other words, the sample mean ought to be close to the population mean, the sample proportion ought to be close to the population proportion, and the sample standard deviation should be close to the population standard deviation. Thus, a good point estimator for the population standard deviation is s.
For a quantitative variable in a particular population, how many different sample means are there?
The sample mean is the mean of a set of sample values taken from a population. Samples drawn from a population may vary in size and contain different data values. Thus, a quantitative variable in a particular population can have many different sets of sample values and there can be many sample means.
Which of the following is a good point estimator for the population mean?
Statistical inference uses statistics calculated from samples as the basis of an inference about the population. If the sample is representative, then the sample statistics (which are random variables that depend on which random sample is selected) ought to be close to their population counterparts. In other words, the sample mean ought to be close to the population mean, the sample proportion ought to be close to the population proportion, and the sample standard deviation should be close to the population standard deviation. Thus, a good point estimator for the population mean is x¯.
A quality control expert at Glotech computers wants to test their new monitors. The production manager claims they have a mean life of 93 months with a standard deviation of 9 months.
If the claim is true, what is the probability that the mean monitor life would be greater than 91.4 months in a sample of 66 monitors? Round your answer to four decimal places.
first, find the standard error
If the claim is true, what is the probability that the mean monitor life would be greater than 91.4 months in a sample of 66 monitors? Round your answer to four decimal places.
first, find the standard error
Assume the population from which the sample is drawn is extremely large. The distribution of x‾ would then be normal with μx‾=μ=93.
σ=Standard Deviation of the population=9
n=Sample Size=66
σx‾=√σ2/n= σ/√n = 9/√66 ≈ 1.107823
P(x‾>91.4)=P(x‾−μ/σx‾>91.4−93/1.107823) =P(z>91.4−93/1.107823)
≈P(z>−1.44)
Correct Answer:0.9251
σ=Standard Deviation of the population=9
n=Sample Size=66
σx‾=√σ2/n= σ/√n = 9/√66 ≈ 1.107823
P(x‾>91.4)=P(x‾−μ/σx‾>91.4−93/1.107823) =P(z>91.4−93/1.107823)
≈P(z>−1.44)
Correct Answer:0.9251
A production manager at a wall clock company wants to test their new wall clocks. The designer claims they have a mean life of 15 years with a variance of 25.
If the claim is true, in a sample of 41 wall clocks, what is the probability that the mean clock life would be greater than 15.4 years? Round your answer to four decimal places.
If the claim is true, in a sample of 41 wall clocks, what is the probability that the mean clock life would be greater than 15.4 years? Round your answer to four decimal places.
√25=5 5/√41≈0.7809
15.4-15=.4/0.7809
Correct Answer:0.3043
15.4-15=.4/0.7809
Correct Answer:0.3043
The mean per capita income is 18,904 dollars per annum with a standard deviation of 469 dollars per annum.
What is the probability that the sample mean would be less than 18850 dollars if a sample of 333 persons is randomly selected? Round your answer to four decimal places.
What is the probability that the sample mean would be less than 18850 dollars if a sample of 333 persons is randomly selected? Round your answer to four decimal places.
469/√333≈25.7010
18850-18,904=-54/25.7010
≈P(z<−2.10)
Correct Answer: 0.0178
18850-18,904=-54/25.7010
≈P(z<−2.10)
Correct Answer: 0.0178
A racing car consumes a mean of 86 gallons of gas per race with a standard deviation of 7 gallons.
If 41 racing cars are randomly selected, what is the probability that the sample mean would be greater than 84.1 gallons? Round your answer to four decimal places.
If 41 racing cars are randomly selected, what is the probability that the sample mean would be greater than 84.1 gallons? Round your answer to four decimal places.
7/√41≈1.0932
84.1-86/1.0932
≈P(z>−1.7380)
Correct Answer: 0.9589
84.1-86/1.0932
≈P(z>−1.7380)
Correct Answer: 0.9589
The mean weight of an adult is 76 kilograms with a variance of 100.
If 142 adults are randomly selected, what is the probability that the sample mean would differ from the population mean by more than 1.5 kilograms? Round your answer to four decimal places.
If 142 adults are randomly selected, what is the probability that the sample mean would differ from the population mean by more than 1.5 kilograms? Round your answer to four decimal places.
√100=10
10/√142≈0.8391813583
Since the true value of the population mean is 76, the value of x‾ should not fall between 74.5 and 77.5 in order for the error of estimation to be more than 1.5.
Correct Answer: 0.0739
10/√142≈0.8391813583
Since the true value of the population mean is 76, the value of x‾ should not fall between 74.5 and 77.5 in order for the error of estimation to be more than 1.5.
Correct Answer: 0.0739
The cost of 5 gallons of ice cream has a standard deviation of 7 dollars with a mean of 39 dollars during the summer.
What is the probability that the sample mean would differ from the true mean by more than 1.2 dollars if a sample of 188 5-gallon pails is randomly selected? Round your answer to four decimal places.
What is the probability that the sample mean would differ from the true mean by more than 1.2 dollars if a sample of 188 5-gallon pails is randomly selected? Round your answer to four decimal places.
7/√188=0.5105274702
Since the true value of the population mean is 39, the value of x‾ should not fall between 37.8 and 40.2 in order for the error of estimation to be more than 1.2 dollars.
Correct Answer: 0.0187
Since the true value of the population mean is 39, the value of x‾ should not fall between 37.8 and 40.2 in order for the error of estimation to be more than 1.2 dollars.
Correct Answer: 0.0187
Thompson and Thompson is a steel bolts manufacturing company. Their current steel bolts have a mean diameter of 139mm, and a variance of 64.
If a random sample of 41 steel bolts is selected, what is the probability that the sample mean would differ from the population mean by more than 2.1mm? Round your answer to four decimal places.
If a random sample of 41 steel bolts is selected, what is the probability that the sample mean would differ from the population mean by more than 2.1mm? Round your answer to four decimal places.
√64=8
8/√141=1.249390095
Since the true value of the population mean is 139, the value of x‾ should not fall between 136.9 and 141.1 in order for the error of estimation to be more than 2.1mm.
Correct Answer: 0.0928
8/√141=1.249390095
Since the true value of the population mean is 139, the value of x‾ should not fall between 136.9 and 141.1 in order for the error of estimation to be more than 2.1mm.
Correct Answer: 0.0928
The mean life of a television set is 119 months with a standard deviation of 14 months.
If a sample of 74 televisions is randomly selected, what is the probability that the sample mean would differ from the true mean by less than 1.1 months? Round your answer to four decimal places.
If a sample of 74 televisions is randomly selected, what is the probability that the sample mean would differ from the true mean by less than 1.1 months? Round your answer to four decimal places.
14/√74=1.627466942
Since the true value of the population mean is 119, the value of x‾ should not fall between 117.9 and 120.1 in order for the error of estimation to be more than 1.1.
Correct Answer: 1.627466942
Since the true value of the population mean is 119, the value of x‾ should not fall between 117.9 and 120.1 in order for the error of estimation to be more than 1.1.
Correct Answer: 1.627466942
The quality control manager at a computer manufacturing company believes that the mean life of a computer is 120 months, with a standard deviation of 10 months.
If he is correct, what is the probability that the mean of a sample of 90 computers would be less than 117.13 months? Round your answer to four decimal places.
If he is correct, what is the probability that the mean of a sample of 90 computers would be less than 117.13 months? Round your answer to four decimal places.
10/√90=1.054092553
Correct Answer: 0.0032
Correct Answer: 0.0032
Thompson and Thompson is a steel bolts manufacturing company. Their current steel bolts have a mean diameter of 133 millimeters, and a standard deviation of 6 millimeters.
If a random sample of 43 steel bolts is selected, what is the probability that the sample mean would be greater than 132.4 millimeters? Round your answer to four decimal places.
If a random sample of 43 steel bolts is selected, what is the probability that the sample mean would be greater than 132.4 millimeters? Round your answer to four decimal places.
6/√43=0.914991422
Correct Answer: 0.7440
Correct Answer: 0.7440
Suppose the horses in a large stable have a mean weight of 1467lbs, and a standard deviation of 93lbs.
What is the probability that the mean weight of the sample of horses would differ from the population mean by less than 9lbs if 49 horses are sampled at random from the stable? Round your answer to four decimal places.
What is the probability that the mean weight of the sample of horses would differ from the population mean by less than 9lbs if 49 horses are sampled at random from the stable? Round your answer to four decimal places.
93/√49=13.28571429
Since the true value of the population mean is 1467, the value of x‾ must fall between 1458 and 1476 in order for the error of estimation to be less than 9.
Correct Answer: 0.5019
Since the true value of the population mean is 1467, the value of x‾ must fall between 1458 and 1476 in order for the error of estimation to be less than 9.
Correct Answer: 0.5019
The mean output of a certain type of amplifier is 287 watts with a standard deviation of 10 watts.
If 56 amplifiers are sampled, what is the probability that the mean of the sample would differ from the population mean by less than 1.8 watts? Round your answer to four decimal places.
If 56 amplifiers are sampled, what is the probability that the mean of the sample would differ from the population mean by less than 1.8 watts? Round your answer to four decimal places.
10/√56=1.33630621
Since the true value of the population mean is 287, the value of x‾ must fall between 285.2 and 288.8 in order for the error of estimation to be less than 1.8.
Correct Answer: 0.8220
Since the true value of the population mean is 287, the value of x‾ must fall between 285.2 and 288.8 in order for the error of estimation to be less than 1.8.
Correct Answer: 0.8220
The operation manager at a tire manufacturing company believes that the mean mileage of a tire is 28,631 miles, with a variance of 16,834,610.
What is the probability that the sample mean would differ from the population mean by less than 219 miles in a sample of 178 tires if the manager is correct? Round your answer to four decimal places.
What is the probability that the sample mean would differ from the population mean by less than 219 miles in a sample of 178 tires if the manager is correct? Round your answer to four decimal places.
√16,834,610=4103.000122
4103.000122/√178=307.5328611
Since the true value of the population mean is 28,631 miles, the value of x‾ must fall between 28412 and 28850 in order for the error of estimation to be less than 219.
Correct Answer: 0.5236
4103.000122/√178=307.5328611
Since the true value of the population mean is 28,631 miles, the value of x‾ must fall between 28412 and 28850 in order for the error of estimation to be less than 219.
Correct Answer: 0.5236
Was this helpful?
Let us know if this was helpful. That’s the only way we can improve.
