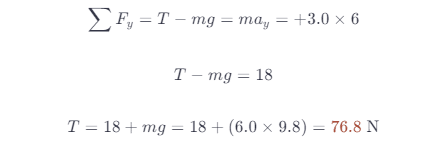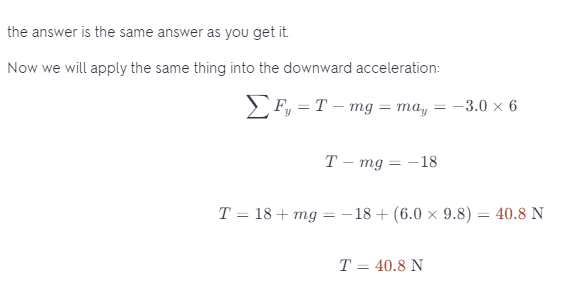A 6kg bucket of water is being pulled straight up by a string at a constant speed. I determined that the tension on the string was F = ma
F = (6kg * 9.8 m/s2), F = 58.8 N
Now it’s asking At a certain point the speed of the bucket begins to change. The bucket now has an upward constant acceleration of magnitude 3 m/s2. What is the tension in the rope now? The correct answer was “about 78N” Then, assume that the bucket has a downward acceleration with a constant acceleration of magnitude 3 m/s2. Now, what is the tension in the rope?
Answer: 76.8 N
Explanation
For the first part of the equation: you solved it right. Note that, usually use Newton’s second law in this kind of problem.
What you did in the first part is the following:

If you choose the upward to be the positive direction, then you should stick with that sign when you are solving.
The force of the tension is positive in the two cases because it is directed up and the force of the weight is negative because it is directed down.
So do the acceleration. When the bucket has an upward acceleration, it means that it has a positive value Ay = +3 m/s^2
And when it has a downward acceleration, it means that it has a negative value of Ay = -3 m/s^2.
Now, you can solve for the second part and the third part easily by using Newton’s second law, as I mentioned above.
Upward acceleration.