Question: The refracted index of water is 1.33. Calculate its critical angle.
Answer: The critical angle for water, with a refractive index of 1.33, is approximately 48.75.
Water, a substance essential for life, exhibits intriguing properties when it comes to light refraction. One such property is its critical angle, which is a fundamental concept in the study of optics.
The critical angle occurs when a ray of light inside a medium, such as water, hits the boundary of a less dense medium, like air, at a specific angle, beyond which all the light is reflected back into the water. This phenomenon is known as total internal reflection.
To calculate the critical angle for water, we must first consider its refractive index, a measure of how much light bends, or refracts, when entering a medium. The refractive index of water is approximately 1.33. Using this value, we can determine the critical angle through a straightforward formula:
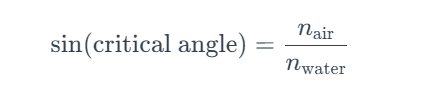
Where n_air is the refractive index of air (approximately 1), and n_water is the refractive index of water.
After applying this formula, we find that the critical angle for water is approximately 48.75∘. This means that when a ray of light inside water strikes the water-air boundary at an angle greater than 48.75∘ with respect to the normal (a line perpendicular to the surface), it will be totally internally reflected.
Understanding the critical angle is not only crucial for academic purposes but also finds practical applications in various fields, including fiber optics, underwater photography, and even in explaining natural phenomena like the sparkling beauty of diamonds and the mysterious appearance of mirages.
In conclusion, the critical angle of water, a seemingly simple concept, opens a window to a fascinating world of optical phenomena, demonstrating the elegant interplay between light and the materials it encounters.



