Home/ Questions/Q 18628
Next
In Process

Quizzma Latest Questions

In:

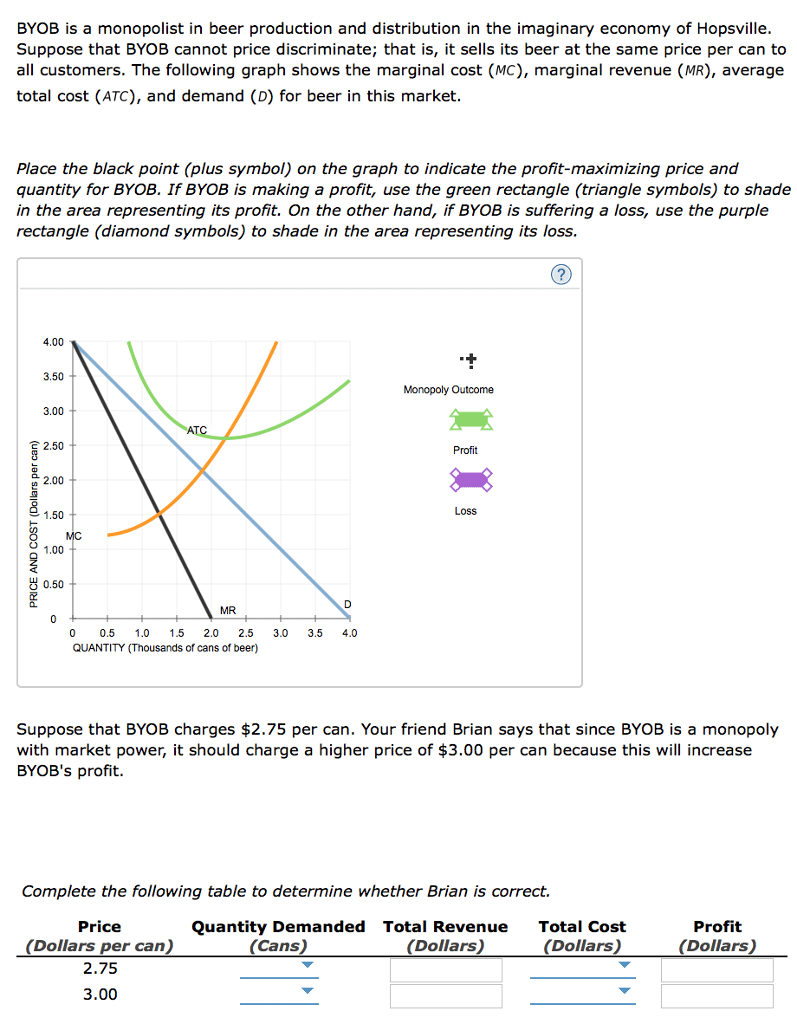
BYOB is a monopolist in beer production

Anonymous

byob is a monopolist in beer production

BYOB is a monopolist in beer production and distribution in the imaginary economy of Hopsville. Suppose that BYOB cannot price discriminate; that is, it sells its beer at the same price per can to all customers.

The following graph shows the marginal cost (MC), marginal revenue (MR), average total cost (ATC), and demand (D) for beer in this market.

Place the black point (plus symbol) on the graph to indicate the profit-maximizing price and quantity for BYOB. If BYOB is making a profit, use the green rectangle (triangle symbols) to shade in the area representing its profit.

On the other hand, if BYOB is suffering a loss, use the purple rectangle (diamond symbols) to shade in the area representing its loss.




Share
    Leave an answer

    Leave an answer

    Browse

    1 Answer

    1. Quizzma Team

      Step-by-Step Analysis:

      1. Identifying the Profit-Maximizing Quantity and Price:
        • The profit-maximizing quantity for a monopolist is where Marginal Revenue (MR) equals Marginal Cost (MC). On the graph, this is the point where the MR and MC curves intersect.
        • From the graph, this intersection appears to occur at approximately 1.5 thousand cans of beer.
        • To determine the corresponding price, follow the vertical line up from this quantity to the demand (D) curve. This price seems to be around $2.75 per can.
      2. Shading the Profit Area:
        • The area representing profit is the rectangle between the demand curve (price), the average total cost curve (ATC), and the quantity axis.
        • At 1.5 thousand cans and $2.75 per can, the ATC seems to be slightly lower than $2.75, indicating that there is some profit.
      3. Completing the Table:

        Price: $2.75 per can

        • Quantity Demanded: 1,500 cans (since this is the profit-maximizing quantity)
        • Total Revenue: $2.75 * 1,500 = $4,125
        • Total Cost: ATC at 1,500 cans is approximately $2.50 per can (estimated from the graph), so Total Cost = $2.50 * 1,500 = $3,750
        • Profit: Total Revenue – Total Cost = $4,125 – $3,750 = $375

        Price: $3.00 per can

        • To find the quantity demanded at $3.00, locate the point on the demand curve at a price of $3.00. This looks to be around 1.25 thousand cans.
        • Quantity Demanded: 1,250 cans
        • Total Revenue: $3.00 * 1,250 = $3,750
        • Total Cost: ATC at 1,250 cans is approximately $2.60 per can (estimated from the graph), so Total Cost = $2.60 * 1,250 = $3,250
        • Profit: Total Revenue – Total Cost = $3,750 – $3,250 = $500

      Conclusion:

      Comparing the profits:

      • At a price of $2.75 per can, the profit is $375.
      • At a price of $3.00 per can, the profit is $500.

      Therefore, Brian is correct. Charging a higher price of $3.00 per can would increase BYOB’s profit from $375 to $500.

    Related Questions