Levels of Measurement Quiz
Levels of Measurement Answers
1. Indicate which level of measurement is being used in the given scenario. The teacher of a class of third graders records the height of each student.
- Nominal
- Ordinal
- Interval
- Ratio
2. Indicate which level of measurement is being used in the given scenario. The teacher of a class of third graders records the eye color of each student.
- nominal
- ordinal
- interval
- ratio
3. Indicate which level of measurement is being used in the given scenario. The teacher of a class of third graders records the letter grade for mathematics for each student.
- nominal
- ordinal
- interval
- ratio
4. Indicate which level of measurement is being used in the given scenario. The teacher of a class of third graders records the percentage that each student got correct on the last science test.
- nominal
- ordinal
- interval
- ratio
5. Indicate which level of measurement is being used in the given scenario. A meteorologist compiles a list of temperatures in degrees Celsius for the month of May.
- nominal
- ordinal
- interval
- ratio
6. Indicate which level of measurement is being used in the given scenario. A meteorologist compiles a list of temperatures in degrees Fahrenheit for the month of May.
- nominal
- ordinal
- interval
- ratio
7. Indicate which level of measurement is being used in the given scenario. A film critic lists the top 50 greatest movies of all time.
- nominal
- ordinal
- interval
- ratio
8. Indicate which level of measurement is being used in the given scenario. A car magazine lists the most expensive cars for 2017.
- nominal
- ordinal
- interval
- ratio
9. Indicate which level of measurement is being used in the given scenario. The roster of a basketball team lists the jersey numbers for each of the players.
- nominal
- ordinal
- interval
- ratio
10. Indicate which level of measurement is being used in the given scenario. A local animal shelter keeps track of the breeds of dogs that come in.
- nominal
- ordinal
- interval
- ratio
11. Indicate which level of measurement is being used in the given scenario. A local animal shelter keeps track of the weights of dogs that come in.
- nominal
- ordinal
- interval
- ratio
12. Is the following qualitative or quantitative data? Favorite foods of statistics class.
- Qualitative
- Quantitative
13. Is the following qualitative or quantitative data? Breeds of dogs owned by CHS Seniors.
- Qualitative
- Quantitative
14. Is the following qualitative or quantitative data? Age of statistics parent or guardians.
- Qualitative
- Quantitative
15. Determine the level of measurement. Weight of walleye caught on Lake Erie
- Nominal
- Ordinal
- Interval
- Ratio
16. Determine the level of measurement. List of popular video games
- Nominal
- Ordinal
- Interval
- Ratio
17. Determine the level of measurement. Height of students in inches
- Nominal
- Ordinal
- Interval
- Ratio
18. Determine the level of measurement. Hourly wages of students in fastfood.
- Nominal
- Ordinal
- Interval
- Ratio
19. Determine the level of measurement. Popular baby names in 2017
- Nominal
- Ordinal
- Interval
- Ratio
20. Determine the level of measurement. Birth year of employees at your work
- Nominal
- Ordinal
- Interval
- Ratio
21. Temperature of the body expressed in Kelvin
- Nominal
- Ordinal
- Interval
- Ratio
22. Number of students in the classroom
- Nominal
- Ordinal
- Interval
- Ratio
23. Ages of students in a statistics class
- Nominal
- Ordinal
- Interval
- Ratio
24. A ___________ is a characteristic that we observed and measured from every element of the universe.
- Data
- Variable
- Observation
- Value
25. A qualitative variable
- A. Always refers to a sample
- B. Is not numeric
- C. Has only two possible outcomes
- D. All of the above are correct
26. The ratio scale of measurement
- A. Usually involves ranking
- B. Cannot assume negative values
- C. Has a meaningful zero point
- D. Is usually based on counting
27. The ordinal scale of measurement
- A. Has a meaningful zero point
- B. Is based on ranks
- C. Cannot assume negative values
- D. All of the above
28. A part of the population.
- biased sample
- population
- random sample
- sample
29. The entire group of objects or individuals considered for a survey.
- biased sample
- population
- random sample
- sample
30. ___________ consists of numbers representing counts or measurements.
- Mathematical data
- Categorical data
- Quantitative data
- Population data
Levels of Measurement Examples and Terms to Learn
Ordinal
Interval
Ratio
The precision and properties of the data are related to the level of measurement
Tells you the if there is a similarity or difference (we have one male and one female)
Categories (gender, SES), identifiers, names, labels
More qualitative variables since numbers serve to identify
Numbers are assigned arbitrarily to these categories
There really isn’t a numerical meaning
Male – 1
Female – 2
Transgendered – 3
You can’t say a 1 is less than a 3 or a 3 is one more than a 2
All numbers are equal
**Classifying and counting
Ex. Sex, eye color, zip code, I’d number
****Use with MODE
Tells you if the numbers are equal or not but doesn’t tell you the magnitude
Values can be ordered or ranked from high to low, best to worst, or least to greatest, tallest to shortest, strongly disagree to strongly agree, etc.
**classifying counting and ranking
Ex. Hardness of minerals (good, better, best), grades
****Use with MEDIAN
Grading scales (e.g., A, B, C) have order but lack other properties
Voice quality (e.g., 0 = normal while 3 = extreme)
Cannot say a 4 on a Likert Scale twice as good as a 2
Not a precise way of measuring something
Do not have the property of equal intervals
In their raw form, ordinal data are not suitable for statistical analysis
There are equal intervals (equidistant points) between data points (e.g., standard scores)
Able to describe magnitude
Able to add and subtract but not able to multiply and divide the data
Since there is no zero, there is no absence of the property being measured (IQ, language)
**Classifying counting ranking addition subtraction
Ex. Calendar dates, temperature, dress size
****Symettrical data: MEAN
****Skewed data: MEDIAN
Numbers have the property of inequality
Able to judge the magnitude
There are equal intervals between data points
There is an absolute zero (an absence of that property)
Able to add, subtract, multiply and divide the data
Length, width, height, speaking rate, words read per minute, number of dysfluencies
Classifying counting ranking addition subtraction multiplication division has a true zero
Ex. Number of patients seen, age, length
****Symmetrical data: Mean
****Skewed data: Median
Measures of location (Mean, median, mode)
Measures of Individual Location (Ranks, percentile ranks, standard scores)
Measures of Variability
Range
Variance
Standard Deviation
Coefficient of Variance
Can just express data in terms of mean, median, and mode without variability information.
Information is lost when this happens
See a degree of dispersion in a data set (i.e., variability or spread)
Number of different categories for nominal data (e.g., number of SES is divided by only 2 categories vs. 7)
If the SD is large, the values are spread further away from the mean
Ex. Ranks, percentile ranks, standard scores
Best if used for ordinal data
Measure of score variation
Difference between the lowest and highest score
12 9 15 24 20 8 11 21 22 14
Highest Lowest
Range is 24 – 8= 16
Allows you to represent data as it is dispersed around the mean
If the SD is large, the values are spread further away from the mean
Allows you to express a standard deviation as a percentage
Good when you compare 2 sets of data
Sum the scores and divide by the number of participants or entities in the data set
Best way to estimate a population parameter when compared to the other measures of central tendency
Influenced by extreme scores
Point above and below which half the scores fall (i.e., middle value in a list of numbers)
2 5 8 8 12 14 15 17 19 (12 is the median)
2 5 8 8 12 14 15 17 19 20 (12 and 14 are averaged to get median)
Not influenced by extreme scores
Used when the data set contains a few extreme scores
Describes typical salary levels since an average would be affected by outliers (i.e., billioniares)
If no number is repeated, there is no mode
1 1 1 1 8 9 12 14 15 17 19 20
The most frequently occurring responses on the survey was 5 (strongly agree)
Most frequent score on a test
Describes the spread of the scores around the mean
The larger the standard deviation (SD), the more spread out the scores
The smaller the SD, the closer the scores to the mean
All variables have distributions (or patterns of occurrence)
Tells us how often different values should occur on the distribution if samples of the same size are collected over and over from the same population
The shape of the distribution can be interpreted since it affects which statistical analysis you use
Researchers don’t typically report these
Most try to transform the data statistically to approximate a normal distribution in order to do some further statistical analyses
Three types: Unimodal, bimodal, and skewed
Simplifies the data’s structure
Makes the distribution more symmetrical (the goal)
Addresses variability in data
Make relationships more linear
*If there is an outlier and the rest test 68% interval. Random assignment failed so they did not have initial group equivalency. Go back and run numbers. Can attribute this to the outliers.
-Use logarithms, inverse operations, or square root transformations to transform the data
Visual inspection of the distribution data will help identify
Examination of the skew and kurtosis
Inferential tests of normality (e.g., Kolmorogov-Smirnov) with help identify
Best to combine visual inspection and objective tests to evaluate normality
**Blind the administrator to try and avoid this
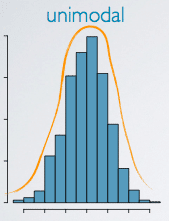
Bell shaped curve
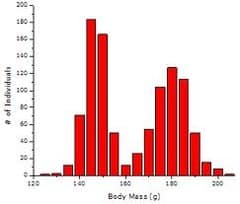
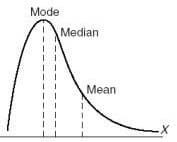
They are not normally distributed
Not symmetrical
Can be positive or negative
-We don’t want this because it means that there are outliers.
*Image is positively skewed
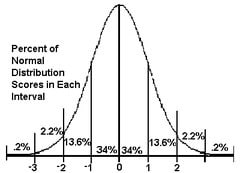
Used for determining the probability of certain outcomes
Is unimodal (one mode in the center)
Is symmetrical
Is continuous
Is asymptotic (i.e., gets closer to the horizonal axis as it moves away from the center but never touches the axis)
68% will be within 1 standard deviation (e.g., average range)
95% will fall within 2 standard deviations
99% will fall within 3 standard deviations
a) Continuous Variables
b) Discrete Variables
c) Dichotomous Variables
a) Continuous Variables
b) Discrete Variables
c) Dichotomous Variables
a) Continuous Variables
b) Discrete Variables
c) Dichotomous Variables
2. Ordinal
3. Interval
4. Ratio
a) Nominal
b) Ordinal
c) Interval
d) Ratio
a) Nominal
b) Ordinal
c) Interval
d) Ratio
a) Nominal
b) Ordinal
c) Interval
d) Ratio
a) Nominal
b) Ordinal
c) Interval
d) Ratio
a) Nominal
b) Ordinal
c) Interval
d) Ratio
a) Nominal
b) Ordinal
c) Interval
d) Ratio
a) Nominal
b) Ordinal
c) Interval
d) Ratio
a) Nominal
b) Ordinal
c) Interval
d) Ratio
a) Nominal
b) Ordinal
c) Interval
d) Ratio
a) Nominal
b) Ordinal
c) Interval
d) Ratio




