Frank shows that triangle A is congruent to triangle B by rotating triangle A around point J and then translating it so it matches up with triangle B exactly. Which conclusion can be drawn from Frank’s transformations?
If one pair of angles is congruent, then all pairs of angles are congruent.
If two pairs of sides and the included angle are congruent, the triangles are congruent.
If two triangles have right angles, all pairs of corresponding sides are congruent.
If right triangles have congruent hypotenuses and one pair of congruent legs, the triangles are congruent.

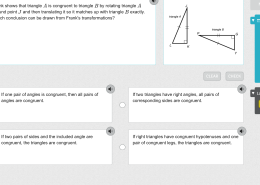
The correct conclusion that can be drawn from Frank’s transformations is: If two triangles have right angles, all pairs of corresponding sides are congruent.
Explanation: When triangle A is rotated and translated to match triangle B exactly, it means that all corresponding sides and angles of both triangles are congruent. This transformation confirms that the triangles have the same geometric properties. Because they can be made to overlap perfectly, all corresponding sides and angles must be congruent as well. This illustrates the essential principle that if triangles can be transformed to coincide exactly, they are congruent overall. If you’d like to explore this further, check the extended services page for more in-depth assistance!