Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
Using the data shown on the graph, which statements are correct?
A The ratio of x y is 6 5.
B The ratio of y x is consistent.
C The graph represents a proportional relationship.
D The graph does not represent a proportional relationship.
E The graph of a proportional relationship must past through (0, 0).
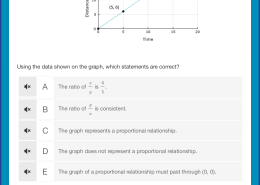
To determine which statements are correct based on the graph, let’s analyze each statement:
A. The ratio of x to y is 6:5 – This would be correct if you can identify two points on the graph where the ratio of x to y matches this value.
B. The ratio of y to x is consistent – This implies that as y increases, x would also increase at a constant rate, which depends on the graph.
C. The graph represents a proportional relationship – A graph represents a proportional relationship if it is a straight line that passes through the origin (0, 0).
D. The graph does not represent a proportional relationship – This would be correct if the graph does not pass through the origin or is not linear.
E. The graph of a proportional relationship must pass through (0, 0) – This statement is true, as a proportional relationship always starts from the origin.
So, check the graph against these points. If it passes through the origin and shows a constant ratio, then C and E could be correct. Otherwise, consider D and possibly others.
To ensure you have the best answer, take a close look at the details of the graph. Good luck!