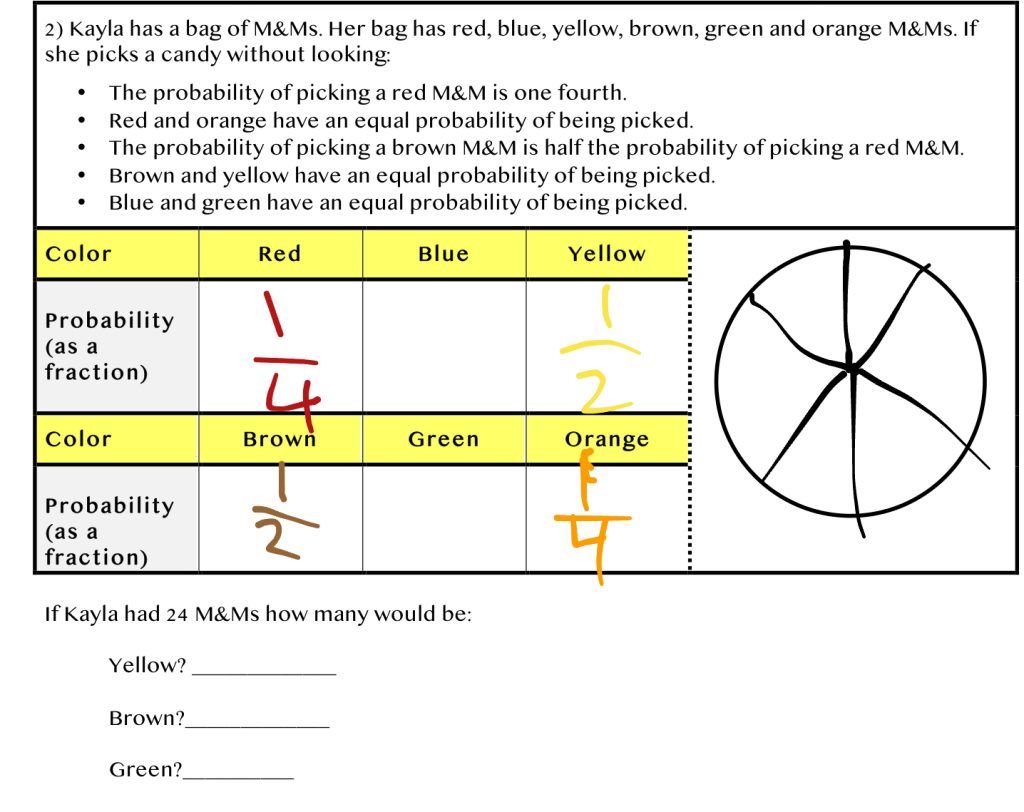
Kayla has a bag of M&Ms. Her bag has red, blue, yellow, brown, green, and orange M&Ms. If she picks a candy without looking:

• The probability of picking a red M&M is one fourth.
• Red and orange have an equal probability of being picked.
• The probability of picking a brown M&M is half the probability of picking a red M&M.
• Brown and yellow have an equal probability of being picked.
• Blue and green have an equal probability of being picked.

If Kayla had 24 M&Ms, how many would be:

1. Yellow? _______
2. Brown? _______
3. Green? _______

Report Content

• Issue: *
  Copyright Infringement Spam Invalid Contents Broken Links
• Your Name: *
  
• Your Email:
  

• Details: *
  

Submit Report