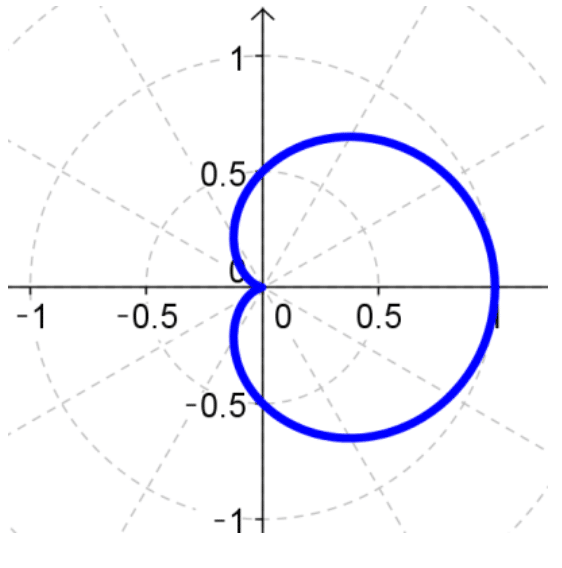
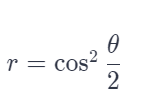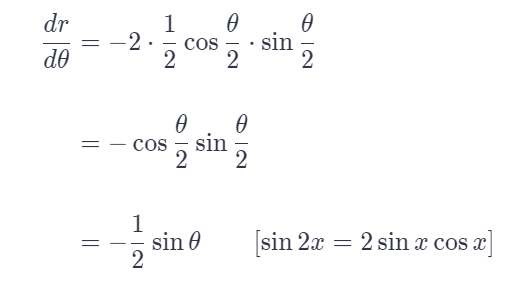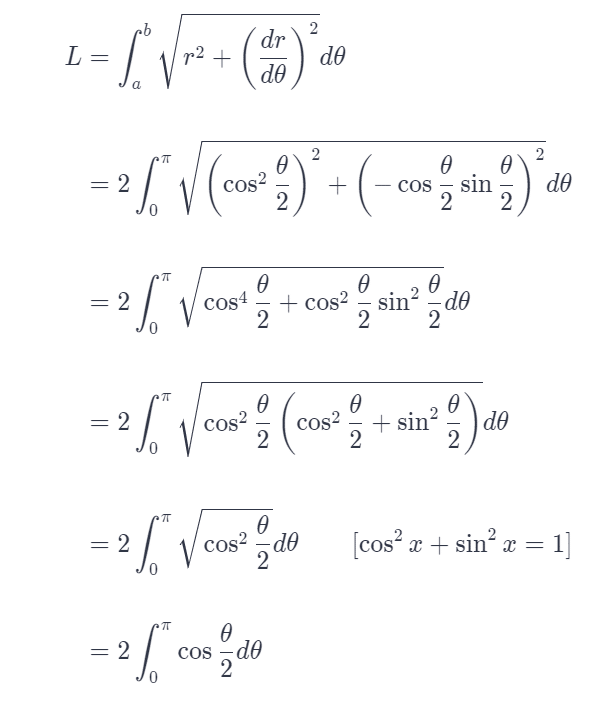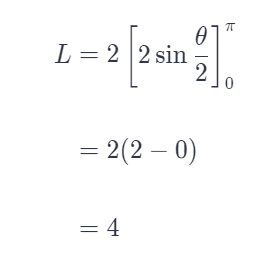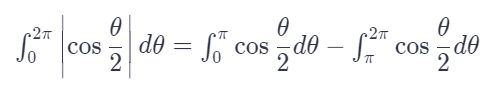Find the exact length of the curve. Use a graph to determine the parameter interval.
r=cos2(θ/2)
Answer: 4
Explanation
Blue graph:
One full figure is completed from 0 < θ < π
Let’s use symmetry and double the integral from 0 to π. This avoids the problem of getting a 0 answer (like problem 49) with parts canceling out.
We won’t use that last double angle formula thing because it will be useful to keep the angles as θ/2 for manipulation.
Use the polar arc length formula:
Right here is where a problem would occur because up to now the integrand was all positive, but would be negative for half the interval from 0 to 2π.
This would turn out to be 0 if we used the upper limit 2π, which would be obviously incorrect.
Technically the proper way to write it after removing the square root symbol instead is:
Which forces us to split the intervals and negate the negative part so we can get the correct answer if we used the entire interval instead of doubling half.