Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
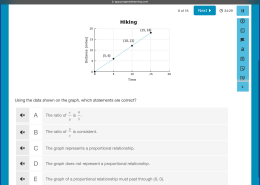
Using the data shown on the graph, which statements are correct?
A. The ratio of x/y is 6/5.
B. The ratio of y/x is consistent.
C. The graph represents a proportional relationship.
D. The graph does not represent a proportional relationship.
E. The graph of a proportional relationship must pass through (0, 0).
To determine which statements are correct based on the graph, let’s analyze each one:
A. The ratio of x/y is 6/5.
This would be true if the graph consistently shows points that maintain this ratio. You would need to check the specific points on the graph to confirm this.
B. The ratio of y/x is consistent.
Similar to statement A, this requires checking the ratios of the y-values to the x-values for the points on the graph. If they remain the same, this statement is true.
C. The graph represents a proportional relationship.
A proportional relationship means that the ratio of y to x is constant and that the line passes through the origin (0,0). If the graph meets these criteria, this statement is correct.
D. The graph does not represent a proportional relationship.
This would be true if the line does not pass through the origin or the ratios are inconsistent. This contradicts statement C.
E. The graph of a proportional relationship must pass through (0, 0).
This statement is true. For a relationship to be proportional, it must include the origin.
You’d need to look at the graph to determine which of the statements A, B, C, and D are correct. Knowing how proportional relationships work will also help you identify the truthfulness of these statements!
Based on standard principles of proportional relationships, the correct answers would likely include statements C and E.
Correct Answers:
Explanation: The graph meets all criteria for a proportional relationship, and the ratio of is consistent across all points.