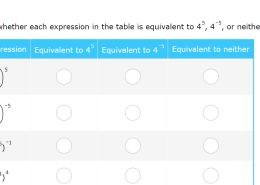
Tell whether each expression in the table is equivalent to

Let’s go through each expression step-by-step.

### Expression 1: ((1/4)^{5})

This is equivalent to ((4^{-1})^{5}), which simplifies to (4^{-5}) (using the property that ((a^m)^{n} = a^{mn})). So, this expression is equivalent to 4 raised to the power of negative 5.

### Expression 2: ((1/4)^{-5})

This can be rewritten as ((4^{-1})^{-5}), which simplifies to (4^{5}). So, this expression is equivalent to 4 raised to the power of 5.

### Expression 3: ((4^{5})^{-1})

By using the property of exponents, this simplifies to (4^{-5}). So, this expression is also equivalent to 4 raised to the power of negative 5.

### Expression 4: ((4^{1})^{4})

Using the exponent rule again, this simplifies to (4^{4}). This expression is neither equivalent to (4^{5}) nor (4^{-5}).

### Summary:

– Expression 1: 4 raised to the power of negative 5

– Expression 2: 4 raised to the power of 5

– Expression 3: 4 raised to the power of negative 5

– Expression