Find the coordinates of the vertices of each figure after the given transformation.

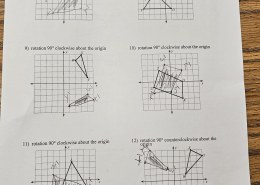
To find the coordinates of the vertices after the specified rotations about the origin, you can follow these transformation rules:

1. Rotation 180° about the origin: The coordinates ((x, y)) become ((-x, -y)).
2. Rotation 90° clockwise about the origin: The coordinates ((x, y)) become ((y, -x)).
3. Rotation 90° counterclockwise about the origin: The coordinates ((x, y)) become ((-y, x)).

Given specific vertices of a figure (which you haven’t provided), you would apply the transformations as follows for any vertex ((x, y)):

– For rotation 180°: Change to ((-x, -y)).

– For 90° clockwise: Change to ((y, -x)).

– For 90° counterclockwise: Change to ((-y, x)).

If you provide specific vertices, I can walk you through the calculations more precisely! Check the extended services page for additional detailed assistance if needed.