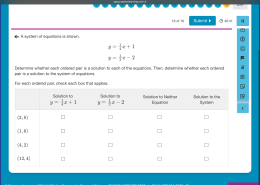
Determine whether each ordered pair is a solution to each of the equations. Then, determine whether each ordered pair is a solution to the system of equations.
For each ordered pair, check each box that applies.
Solution to y = (1/4)x + 1
Solution to y = (1/2)x – 2
Solution to Neither Equation
Solution to the System

To determine whether each ordered pair is a solution to the given equations, you will need to substitute the values of each ordered pair (x, y) into both equations and check if the resulting statements are true (i.e., if both sides of the equations are equal).
Let’s say the ordered pairs are (x₁, y₁) and (x₂, y₂). Here are the steps to follow:
1. Check the first equation: y = (1/4)x + 1
– Substitute x₁ into the equation and see if y₁ equals (1/4)x₁ + 1.
2. Check the second equation: y = (1/2)x – 2
– Substitute x₁ into this equation and see if y₁ equals (1/2)x₁ – 2.
3. Repeat steps 1 and 2 for the second ordered pair (x₂, y₂).
4. Determine if the ordered pairs are solutions by marking the appropriate checkboxes based on the outcomes of your substitutions.
If both equations hold true for an ordered pair, then it is a solution to the system of equations.
Once you’ve completed these steps for your specific ordered pairs, you can categorize them based on the correctness of your substitutions. If you need help with specific ordered pairs, please share them!